System binarny, znany również jako system dwójkowy, jest podstawą nowoczesnej technologii komputerowej. Składa się z dwóch cyfr: 0 i 1, co sprawia, że jest kluczowy dla działania wszystkich urządzeń cyfrowych. Aby umiejętnie przeprowadzać obliczenia w tym systemie, niezbędne jest zrozumienie, jak konwertować liczby między systemem binarnym a dziesiętnym oraz jak wykonywać podstawowe działania arytmetyczne.
W artykule przedstawione zostaną proste metody konwersji liczb dziesiętnych na binarne oraz odwrotnie. Omówimy także zasady dodawania, odejmowania, mnożenia i dzielenia w systemie binarnym, co pozwoli lepiej zrozumieć jego zastosowanie w praktyce. Dzięki tym informacjom, każdy będzie mógł łatwo poruszać się po świecie systemu binarnego.
Najważniejsze informacje:- System binarny składa się z cyfr 0 i 1, co jest podstawą technologii komputerowej.
- Aby zamienić liczbę dziesiętną na binarną, można użyć metody potęg liczby 2 lub dzielenia przez 2.
- Konwersja z systemu binarnego na dziesiętny polega na mnożeniu cyfr przez odpowiednie potęgi liczby 2.
- W systemie binarnym dodawanie, odejmowanie, mnożenie i dzielenie odbywa się według zasad podobnych do tych w systemie dziesiętnym.
- Znajomość tych zasad jest kluczowa dla efektywnego korzystania z systemu binarnego w praktyce.
Jak skutecznie zamienić liczby dziesiętne na system binarny
Aby zamienić liczby dziesiętne na system binarny, istnieją dwie popularne metody, które można łatwo zastosować. Obie z nich są skuteczne, ale różnią się podejściem. W tej sekcji omówimy te metody, aby każdy mógł je zrozumieć i wykorzystać w praktyce.
Pierwsza metoda polega na wykorzystaniu potęg liczby 2. W tym przypadku porównujemy wartość liczby dziesiętnej z kolejnymi potęgami liczby 2 (2⁰, 2¹, 2² itd.), a odpowiednie potęgi są dodawane, aby uzyskać pożądaną liczbę. Druga metoda, znana jako dzielenie przez 2, polega na dzieleniu liczby dziesiętnej przez 2 i zapisywaniu reszt z dzielenia, co pozwala na uzyskanie wyniku od dołu do góry. Obie metody są proste i skuteczne, a wybór jednej z nich zależy od preferencji użytkownika.
Metoda potęg liczby 2: krok po kroku dla początkujących
W metodzie potęg liczby 2, zaczynamy od zidentyfikowania największej potęgi liczby 2, która jest mniejsza lub równa danej liczbie dziesiętnej. Na przykład, aby zamienić liczbę 9, analizujemy potęgi liczby 2: 1 (2⁰), 2 (2¹), 4 (2²), 8 (2³). Widzimy, że 8 (2³) jest największą potęgą liczby 2, która nie przekracza 9. Następnie odejmujemy 8 od 9, co daje 1. Ponieważ 1 to 2⁰, zapisujemy 1 w odpowiednim miejscu. Ostatecznie liczba 9 w systemie binarnym to 1001.
Metoda dzielenia przez 2: prosty sposób na konwersję
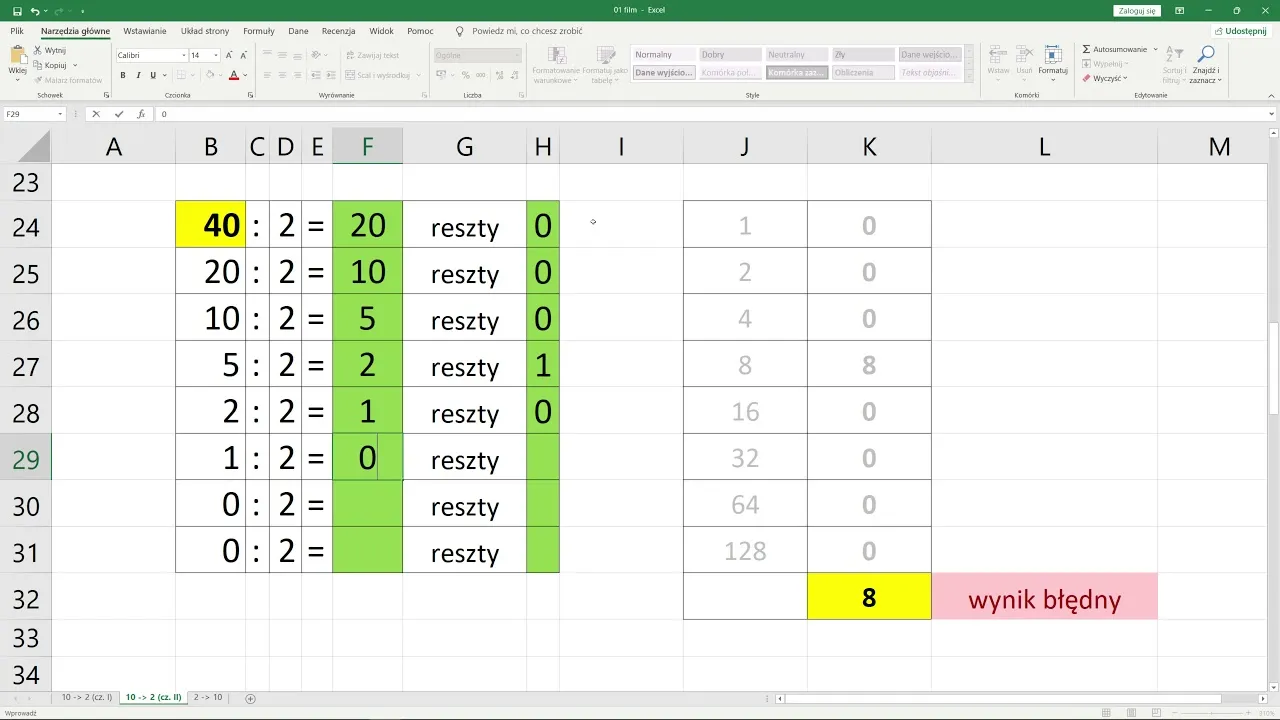
Metoda dzielenia przez 2 polega na powtarzaniu procesu dzielenia liczby dziesiętnej przez 2, zapisując reszty z każdego dzielenia. Na przykład, aby zamienić liczbę 10, dzielimy ją przez 2, co daje 5 i resztę 0. Następnie dzielimy 5 przez 2, co daje 2 i resztę 1, a potem 2 przez 2, co daje 1 i resztę 0. Na końcu, dzieląc 1 przez 2, otrzymujemy 0 i resztę 1. Odczytując reszty od dołu do góry, otrzymujemy 1010, co oznacza, że liczba 10 w systemie binarnym to 1010.
| Metoda | Opis | Zalety | Wady |
|---|---|---|---|
| Potęg liczby 2 | Porównywanie z potęgami liczby 2 | Łatwa do zrozumienia dla początkujących | Może być czasochłonna dla dużych liczb |
| Dzielnie przez 2 | Dzielimy liczbę przez 2, zapisując reszty | Szybka dla dużych liczb | Może być trudniejsza do zrozumienia na początku |
Metoda dzielenia przez 2: prosty sposób na konwersję
Metoda dzielenia przez 2 to jedna z najprostszych i najczęściej stosowanych metod konwersji liczb dziesiętnych na system binarny. Proces polega na dzieleniu liczby dziesiętnej przez 2 i zapisywaniu reszt z każdego dzielenia. Na przykład, aby zamienić liczbę 10 na system binarny, dzielimy ją przez 2, co daje 5 i resztę 0. Następnie dzielimy 5 przez 2, co daje 2 i resztę 1. Kontynuujemy ten proces, aż osiągniemy 0. Ostatnie reszty, odczytane od dołu do góry, stanowią wynik w systemie binarnym.
W przypadku liczby 10, proces wygląda następująco:
- 10 ÷ 2 = 5, reszta 0
- 5 ÷ 2 = 2, reszta 1
- 2 ÷ 2 = 1, reszta 0
- 1 ÷ 2 = 0, reszta 1
Odczytując reszty od dołu do góry, otrzymujemy 1010. W związku z tym, liczba 10 w systemie binarnym to 1010.
Jak przeliczyć liczby binarne na system dziesiętny
Aby zamienić liczby binarne na system dziesiętny, istnieją dwie główne metody, które można zastosować. Obie metody są skuteczne i pozwalają na dokładne przeliczenie wartości. W tej sekcji omówimy te metody, aby ułatwić zrozumienie, jak działa konwersja w odwrotnym kierunku.
Jedną z metod jest mnożenie każdej cyfry liczby binarnej przez odpowiednią potęgę liczby 2. Wartości potęg są ustalane od prawej do lewej, zaczynając od 2⁰. Drugą metodą jest dodawanie wartości odpowiadających poszczególnym cyfrom, które są równe 1. W tej sekcji szczegółowo omówimy obie metody, aby każdy mógł łatwo przeliczać liczby binarne na dziesiętne.
Zasada mnożenia potęg liczby 2: przykład w praktyce
Konwersja liczby binarnej na system dziesiętny polega na mnożeniu każdej cyfry liczby binarnej przez odpowiednią potęgę liczby 2. Zaczynamy od potęgi zerowej (2⁰) i przesuwamy się w lewo, zwiększając potęgę o jeden dla każdej kolejnej cyfrze. Na przykład, aby przeliczyć liczbę binarną 1001, analizujemy każdą cyfrę:
- 1 × 2³ = 8
- 0 × 2² = 0
- 0 × 2¹ = 0
- 1 × 2⁰ = 1
Następnie dodajemy wyniki: 8 + 0 + 0 + 1 = 9. Zatem liczba binarna 1001 odpowiada liczbie dziesiętnej 9.
Jak odczytać liczby binarne: wizualizacja i wyjaśnienie
Odczytywanie liczb binarnych wymaga zrozumienia ich struktury. Liczby binarne składają się z cyfr 0 i 1, a każda cyfra ma swoje miejsce, które odpowiada potędze liczby 2. Najbardziej znacząca cyfra (MSB) znajduje się po lewej stronie, a najmniej znacząca (LSB) po prawej. Na przykład w liczbie binarnej 1010, pierwsza cyfra (1) oznacza 8 (2³), druga cyfra (0) oznacza 0 (2²), trzecia cyfra (1) oznacza 2 (2¹), a ostatnia cyfra (0) oznacza 0 (2⁰). Zrozumienie tej struktury jest kluczowe dla prawidłowego przeliczania i interpretacji wartości binarnych.
Czytaj więcej: Jak przeliczać system binarny: proste metody i przykłady konwersji
Jak wykonywać podstawowe działania arytmetyczne w systemie binarnym
W systemie binarnym, podobnie jak w systemie dziesiętnym, można wykonywać podstawowe działania arytmetyczne, takie jak dodawanie i odejmowanie. Kluczowe różnice polegają na tym, że operacje te odbywają się tylko z użyciem cyfr 0 i 1. W tej sekcji przyjrzymy się zasadom dodawania i odejmowania w systemie binarnym oraz przedstawimy przykłady, które pomogą zrozumieć te operacje.
Dodawanie w systemie binarnym jest procesem, który wymaga uwzględnienia przeniesienia, podobnie jak w systemie dziesiętnym. Na przykład, aby dodać liczby binarne 1011 i 1101, zaczynamy od najmniej znaczącej cyfry (po prawej stronie). Dodajemy 1 + 1, co daje 0 z przeniesieniem 1. Następnie dodajemy 1 (przeniesienie) + 1 + 0, co również daje 0 z przeniesieniem 1. Kontynuując, dodajemy 1 (przeniesienie) + 0 + 1, co daje 0 z przeniesieniem 1. Na końcu dodajemy 1 (przeniesienie) + 1 + 1, co daje 1 z przeniesieniem 1. Ostateczny wynik to 11000.
Dodawanie liczb binarnych: zasady i przykłady
W dodawaniu liczb binarnych stosujemy zasady podobne do dodawania w systemie dziesiętnym, ale z uwzględnieniem tylko cyfr 0 i 1. Główne zasady to:
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 0 (przeniesienie 1)
- 1 + 1 + 1 = 1 (przeniesienie 1)
Na przykład, dodając liczby binarne 1100 i 1010, zaczynamy od prawej strony. 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, a następnie 1 + 1 = 0 z przeniesieniem 1. Ostateczny wynik to 10110.
Odejmowanie w systemie binarnym: krok po kroku
Odejmowanie w systemie binarnym wymaga zrozumienia zasad pożyczania, podobnie jak w systemie dziesiętnym. Proces zaczyna się od najmniej znaczącej cyfry (LSB) i przesuwa się w lewo, stosując zasady dotyczące pożyczek. Na przykład, aby odjąć 1010 od 1101, zaczynamy od prawej strony. W pierwszej kolumnie mamy 1 - 0, co daje 1. W drugiej kolumnie również 0 - 1, co wymaga pożyczki, więc przekształcamy 1 w 0 i dodajemy 2 do 0, co daje 2 - 1 = 1. W trzeciej kolumnie mamy 1 - 0, co daje 1. W ostatniej kolumnie mamy 1 - 1, co daje 0. Ostateczny wynik to 0011.
Jak zrozumieć mnożenie i dzielenie w systemie binarnym
Mnożenie i dzielenie w systemie binarnym są analogiczne do operacji w systemie dziesiętnym, ale z uwzględnieniem tylko cyfr 0 i 1. Mnożenie polega na dodawaniu, a dzielenie na odejmowaniu, co sprawia, że operacje są proste, ale wymagają precyzji. W tej sekcji przyjrzymy się zasadom obu operacji oraz przedstawimy przykłady, które ułatwią zrozumienie tych procesów.
W przypadku mnożenia, bierzemy jedną z liczb i mnożymy ją przez każdą cyfrę drugiej liczby, przesuwając się w lewo, podobnie jak w mnożeniu w systemie dziesiętnym. Na przykład, aby pomnożyć 101 przez 11, zaczynamy od pierwszej cyfry 1, co daje 101. Następnie przesuwamy się w lewo, mnożąc przez 1, co daje 1010. Następnie dodajemy wyniki, co daje 1111.
W przypadku dzielenia, proces polega na odejmowaniu. Na przykład, aby podzielić 1100 przez 10, zaczynamy od lewej strony. 10 mieści się w 11, co daje 1, a reszta to 1. Następnie, przesuwając się w prawo, sprawdzamy 10, co daje 0. Ostatecznie, wynik to 110.
| Operacja | Przykład | Wynik |
|---|---|---|
| Mnożenie | 101 × 11 | 1111 |
| Dzielenie | 1100 ÷ 10 | 110 |
Jak wykorzystać system binarny w programowaniu i technologii
Znajomość systemu binarnego ma kluczowe znaczenie nie tylko dla matematyki, ale także dla programowania i technologii. W wielu językach programowania, takich jak C, Python czy Java, operacje na liczbach binarnych są powszechnie stosowane, zwłaszcza w kontekście optymalizacji algorytmów i manipulacji danymi. Programiści często wykorzystują operacje bitowe (np. AND, OR, XOR) do efektywnego przetwarzania danych, co pozwala na zwiększenie wydajności aplikacji oraz oszczędność pamięci.
Przyszłość technologii, w tym rozwój sztucznej inteligencji i uczenia maszynowego, również opiera się na zrozumieniu systemu binarnego. W miarę jak systemy stają się coraz bardziej złożone, umiejętność pracy z danymi w formacie binarnym staje się niezbędna dla inżynierów i analityków danych. Dodatkowo, techniki konwersji między systemami liczbowymi mogą być wykorzystane w kontekście kompresji danych, co jest kluczowe dla efektywnego przechowywania i przesyłania informacji w erze cyfrowej.
